Tree/Binary Tree in Python DSA

What is a Tree?

A tree is a nonlinear data structure with hierarchical relationships between its elements without having any cycle, it is basically reversed from a real life tree.

Drinks in a cafe has been ordered in a nice hierarchy, which makes it easier for a customer to choose a drink. This is a tree.

Properties:

Represent hierarchical data
Each node has two components : data and a link to its sub category
Base category and sub categories under it.

Why Tree?

Tree data structures allow quicker, easier, access to the data as it is a nonlinear data structure. Another reason to use a tree data structure is to store information that naturally forms a hierarchy. So, if we wanna store hierarchical data like folder structure, organization structure, XML AND HTML data, tree data structure is very useful. The file system on a computer store data in a hierarchical structure.

Tree Terminology

Basic form:

Terminology :

Root : top node without parent (N1)

Edge : a link between parent and child

Leaf : n node which does not have children

Sibling children of a same parent

Ancestor: parent, grandparent, great grand parent of a node

Depth of Node : a length of the path from root to node

Height of node : a length of the path from the node to the deepest node

Depth of tree : depth of root node (it's always 0)

Height of tree : sum of link from root to the last node.

How to create basic tree in Python

class TreeNode: 
    def __init__(self, data, children = []): 
        self.data = data 
        self.children = children 
    def __str__(self. level = 0): 
        ret = " " * level + str(self.data) + "\n" 
        for child in self.children: 
            ret += child.__str__(level + 1) 
        return ret 
    def addChild(self, TreeNode): 
        self.children.append(TreeNode) 

tree = TreeNode('Drinks', []) #empty children 
cold = TreeNode('Cold', []) #empty children 
hot = TreeNode('Hot', []) #empty children 
tree.addChild(cold)
tree.addChild(hot)

tea = TreeNode('Tea', []) 
coffee = TreeNode('Coffee', [])
cola = TreeNode('Cola', []) 
fanta = TreeNode('Fanta', [])

cold.addChild(cola) 
cold.addChild(fanta) 
hot.addChild(tea) 
hot.addChild(coffee) 

print(tree)

Result: Under root node, we have cold and hot drinks. Under cold drinks, we have cola and Fanta. Under hot drinks, we have tea and coffee.

str function for Tree - explanation

def __str__(self, level=0):
        ret = "  " * level + str(self.data)  + "\n"
        for child in self.children:
            ret += child.__str__(level + 1)
            print(ret)
        return ret

Method Signature:

def __str__(self, level=0):

__str__ is the name of the method. The double underscores indicate that it is a special method in Python, often called a "dunder" method (short for "double underscore").

self refers to the instance of the TreeNode object on which this method is called.

level=0 is a parameter with a default value of 0. This is used for keeping track of the tree depth (or the level of indentation) in the string representation.

Initial String Creation:

ret = " " * level + str(self.data) + "\n"

ret is a local variable that starts with the string representation of the tree node's data.

" " * level creates a string of spaces for indentation, where the number of spaces is twice the level value. This helps in visually representing the tree structure.

str(self.data) converts the node's data to a string.

"\n" adds a newline character at the end, ensuring each node's data starts on a new line.

Looping Over Children:

for child in self.children:

This loop iterates over the children list of the current tree node.

Recursive __str__ Call:

ret += child.__str__(level + 1)

For each child, the __str__ method is called recursively (child.__str__(level + 1)).

level + 1 increases the indentation level for the child nodes, indicating that they are one level deeper in the tree.

The string representation of each child (including its own children, if any) is concatenated to the ret variable.

Printing Intermediate ret (Debugging Line):

print(ret)

This line prints the current state of the ret variable after adding each child's string representation. This line seems to be for debugging purposes and will print the partial tree structure as it is built. In a production version of this method, you might want to remove this print statement.

Returning the Final String:

return ret

Finally, after concatenating the string representations of all the children, the ret variable is returned. This is the complete string representation of the tree starting from the current node.

Important Note:

The default parameter children=[] in the __init__ method can lead to unexpected behavior. Mutable default arguments in Python are a common source of bugs. Each instance of TreeNode without explicitly passed children will share the same list, which can lead to children being shared across different tree nodes. It's usually safer to default to None and set children to a new list in the body of the method if it's None.

Binary Tree

One is has been cleared to us, that is we can make unlimited children for one node. But, in binary it's different.

In binary trees, each node can have at most two children often referred to as left and right node. A node cannot have more than two children.
Binary tree is a family of data structure (BST, Heap tree, AVL, red black tree, Syntax tree) their basic property is driven by binary tree property.

Why binary tree?

The first reason is that binary trees are prerequisite for more advanced trees like BST, AVL, Red black trees.
Huffman coding problem, head priority problem and expression parsing problems can be solved efficiently by binary trees.

Types of Binary Tree

Full Binary Tree : If each node of a binary tree has zero or two children, but not one, then this binary tree is full binary tree.

Perfect Binary Tree: All non-leaf nodes have two children and they are at the same depth and all the leaf nodes are located in same level.

Complete Binary Tree: All levels are completely filled except the last level.

Balanced Binary Tree: Each leaf is not more that a certain distance from the root node than any other leaf. It means, all nodes are located in the same distance from the root node.

Binary Tree Representation

Binary tree can be represented in two ways

- Linked list

- Python list (array)

Create Binary Tree (Linked list)

class TreeNode: 
    def __init__(self, data): 
        self.data = data 
        self.leftChild = None 
        self.rightChild = None 
newBT =  TreeNode("Drinks")

Time complexity : O(1)

Space complexity : O(1)

PreOder Traversal Binary Tree (Linked list)

The logic is, Root node -> Left subtree -> Right subtree (visit path)

N1 -> N2 -> N4 -> N9 -> N10 -> N5 -> N3 -> N6 -> N7. The right subtree's right lead will be visited at the end

class TreeNode: 
    def __init__(self, data): 
        self.data = data 
        self.leftChild = None 
        self.rightChild = None 
newBT =  TreeNode("Drinks") 
leftChild = TreeNode("Hot") 
rightChild = TreeNode("Cold")
newBT.leftChild = leftChild 
newBT.rightChild = rightChild

def preOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    print(rootNode.data) #O(1)
    preOrderTraversal(rootNode.leftChild) #O(N/2)
    preOrderTraversal(rootNode.rightChild) #O(N/2)

preOrderTraversal(newBT)

Time complexity : O(N)

Space complexity : O(N)

InOrder Traversal Binary Tree (Linked list)

In case of inOrder traversal, we will visit the left subtree, then root node, then finally right subtree. Left subtree -> root node -> Right subtree

N9 -> N4 -> N10 -> N2 -> N5 -> N1 -> N6 -> N3 -> N7

class TreeNode: 
    def __init__(self, data): 
        self.data = data 
        self.leftChild = None 
        self.rightChild = None 
newBT =  TreeNode("Drinks") 
leftChild = TreeNode("Hot") 
rightChild = TreeNode("Cold")
newBT.leftChild = leftChild 
newBT.rightChild = rightChild

def preOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    print(rootNode.data) #O(1)
    preOrderTraversal(rootNode.leftChild) #O(N/2)
    preOrderTraversal(rootNode.rightChild) #O(N/2)

def inOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    inOrderTraversal(rootNode.leftChild) #O(N/2)
    print(rootNode.data) #O(1)
    inOrderTraversal(rootNode.rightChild)   #O(N/2)

inOrderTraversal(newBT)

Time complexity : O(N)

Space complexity : O(N)

PostOrder Traversal Binary Tree (Linked list)

The visit path is Left subtree -> Right subtree -> Root node

N9 -> N10 -> N4 -> N5 -> N2 -> N6 -> N7 -> N3 -> N1

class TreeNode: 
    def __init__(self, data): 
        self.data = data 
        self.leftChild = None 
        self.rightChild = None 
newBT =  TreeNode("Drinks") 
leftChild = TreeNode("Hot") 
rightChild = TreeNode("Cold")
newBT.leftChild = leftChild 
newBT.rightChild = rightChild

def preOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    print(rootNode.data) #O(1)
    preOrderTraversal(rootNode.leftChild) #O(N/2)
    preOrderTraversal(rootNode.rightChild) #O(N/2)

def inOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    inOrderTraversal(rootNode.leftChild) #O(N/2)
    print(rootNode.data) #O(1)
    inOrderTraversal(rootNode.rightChild)   #O(N/2)

def postOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    postOrderTraversal(rootNode.leftChild) #O(N/2)
    postOrderTraversal(rootNode.rightChild) #O(N/2)
    print(rootNode.data) #O(1)

postOrderTraversal(newBT)

Time complexity : O(N)

Space complexity : O(N)

LevelOrder Traversal Binary Tree (Linked list)

As the name suggests, we traverse the tree level by level. In every level, we will start traversing from left.

N1 -> N2 -> N3 -> N4 -> N5 -> N6 -> N7 -> N9 -> N10

We will create a queue based on the queue that we created in our previous queue blog. We will import it in our code to create level order traversal.

import QueueLinkedList as queue

class TreeNode: 
    def __init__(self, data): 
        self.data = data 
        self.leftChild = None 
        self.rightChild = None 
newBT =  TreeNode("Drinks") 
leftChild = TreeNode("Hot") 
rightChild = TreeNode("Cold")
newBT.leftChild = leftChild 
newBT.rightChild = rightChild

def preOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    print(rootNode.data) #O(1)
    preOrderTraversal(rootNode.leftChild) #O(N/2)
    preOrderTraversal(rootNode.rightChild) #O(N/2)

def inOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    inOrderTraversal(rootNode.leftChild) #O(N/2)
    print(rootNode.data) #O(1)
    inOrderTraversal(rootNode.rightChild)   #O(N/2)

def postOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    postOrderTraversal(rootNode.leftChild) #O(N/2)
    postOrderTraversal(rootNode.rightChild) #O(N/2)
    print(rootNode.data) #O(1)

def levelOrderTraversal(rootNode): 
    if not rootNode:  #checking the rootnode #O(1)
        return
    else: 
        customQueue = queue.Queue()   #O(1)
        customQueue.enqueue(rootNode) #O(1)
        while not (customQueue.isEmpty()): #O(n)
            root = customQueue.dequeue() #O(1)
            print(root.value.data) 
            if (root.value.leftChild is not None): #O(1)
                customQueue.enqueue(root.value.leftChild) 
            if (root.value.leftChild is not None): #O(1)
                customQueue.enqueue(root.value.rightChild)
levelOrderTraversal(newBT)

Time complexity : O(N)

Space complexity : O(N)

Searching for a node in Binary Tree (Linked list)

The idea is very simple. All we have to do is traverse through a binary tree and check if the desired node is there or not. But he question is - which traversal method we should use? We have just now learned 4 different traversing ways. In this case, we will use levelOrder traversal because all the other traversal use stack but levelOrder traverses through queue and we know that queue performs better than stack

import QueueLinkedList as queue

class TreeNode: 
    def __init__(self, data): 
        self.data = data 
        self.leftChild = None 
        self.rightChild = None 
newBT =  TreeNode("Drinks") 
leftChild = TreeNode("Hot") 
rightChild = TreeNode("Cold")
newBT.leftChild = leftChild 
newBT.rightChild = rightChild

def preOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    print(rootNode.data) #O(1)
    preOrderTraversal(rootNode.leftChild) #O(N/2)
    preOrderTraversal(rootNode.rightChild) #O(N/2)

def inOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    inOrderTraversal(rootNode.leftChild) #O(N/2)
    print(rootNode.data) #O(1)
    inOrderTraversal(rootNode.rightChild)   #O(N/2)

def postOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    postOrderTraversal(rootNode.leftChild) #O(N/2)
    postOrderTraversal(rootNode.rightChild) #O(N/2)
    print(rootNode.data) #O(1)

def levelOrderTraversal(rootNode): 
    if not rootNode:  #checking the rootnode #O(1)
        return
    else: 
        customQueue = queue.Queue()   #O(1)
        customQueue.enqueue(rootNode) #O(1)
        while not (customQueue.isEmpty()): #O(n)
            root = customQueue.dequeue() #O(1)
            print(root.value.data) 
            if (root.value.leftChild is not None): #O(1)
                customQueue.enqueue(root.value.leftChild) 
            if (root.value.leftChild is not None): #O(1)
                customQueue.enqueue(root.value.rightChild)

def searchBT(rootNode, nodeValue): 
    if not rootNode: 
        return "The BT does not exist" 
    else: 
        customQueue = queue.Queue() 
        customQueue.enqueue(rootNode) 
        while not (customQueue.isEmpty()): 
            root = customQueue.dequeue() 
            if root.value.data == nodeValue: 
                return "Success"
            if (root.value.leftChild is not None) : 
                customQueue.enqueue(root.value.leftChild) 
            if (root.value.leftChild is not None): 
                customQueue.enqueue(root.value.rightChild)
        return "Not found"

print(searchBT(newBT, "Tea"))     
print(searchBT(newBT, "Green Tea"))

Time complexity : O(N)

Space complexity : O(N)

Inserting a node in Binary Tree (Linked list)

In this case, we have two options here:

A root node is blank
The tree exists and we have to look for a first vacant place

import QueueLinkedList as queue

class TreeNode: 
    def __init__(self, data): 
        self.data = data 
        self.leftChild = None 
        self.rightChild = None 
newBT =  TreeNode("Drinks") 
leftChild = TreeNode("Hot") 
rightChild = TreeNode("Cold")
newBT.leftChild = leftChild 
newBT.rightChild = rightChild

def preOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    print(rootNode.data) #O(1)
    preOrderTraversal(rootNode.leftChild) #O(N/2)
    preOrderTraversal(rootNode.rightChild) #O(N/2)

def inOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    inOrderTraversal(rootNode.leftChild) #O(N/2)
    print(rootNode.data) #O(1)
    inOrderTraversal(rootNode.rightChild)   #O(N/2)

def postOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    postOrderTraversal(rootNode.leftChild) #O(N/2)
    postOrderTraversal(rootNode.rightChild) #O(N/2)
    print(rootNode.data) #O(1)

def levelOrderTraversal(rootNode): 
    if not rootNode:  #checking the rootnode #O(1)
        return
    else: 
        customQueue = queue.Queue()   #O(1)
        customQueue.enqueue(rootNode) #O(1)
        while not (customQueue.isEmpty()): #O(n)
            root = customQueue.dequeue() #O(1)
            print(root.value.data) 
            if (root.value.leftChild is not None): #O(1)
                customQueue.enqueue(root.value.leftChild) 
            if (root.value.leftChild is not None): #O(1)
                customQueue.enqueue(root.value.rightChild)

def searchBT(rootNode, nodeValue): 
    if not rootNode: 
        return "The BT does not exist" 
    else: 
        customQueue = queue.Queue() 
        customQueue.enqueue(rootNode) 
        while not (customQueue.isEmpty()): 
            root = customQueue.dequeue() 
            if root.value.data == nodeValue: 
                return "Success"
            if (root.value.leftChild is not None) : 
                customQueue.enqueue(root.value.leftChild) 
            if (root.value.leftChild is not None): 
                customQueue.enqueue(root.value.rightChild)
        return "Not found"

def insertNodeBT(rootNode, newNode): 
    if not rootNode: 
        rootNode = newNode
    else: 
        customQueue = queue.Queue() 
        customQueue.dequeue(rootNode)
        while not (customQueue.isEmpty()):
            root = customQueue.dequeue()
            if root.value.leftChild is not None: 
                customQueue.enqueue(root.value.leftChild)
            else: 
                root.value.leftChild = newNode 
                return "Successfully Inserted" 

            if root.value.rightChild is not None: 
                customQueue.enqueue(root.value.rightChild) 
            else: 
                root.vallue.leftChild = newNode 
                return "Successfully Inserted" 
newNode = TreeNode("Cola") 
print(insertNodeBT(newBT, newNode)) 
levelOrderTraverse(newBT)

Time complexity : O(N)

Space complexity : O(N)

Delete a node from Binary Tree (Linked list)

( Level order traversal )

We need to keep in mind that, we have to delete a node in a way that will not affect the other nodes that are the children of that node. That's why we will replace the value of deepest node with the node deletng the deepest node.

import QueueLinkedList as queue

class TreeNode: 
    def __init__(self, data): 
        self.data = data 
        self.leftChild = None 
        self.rightChild = None 
newBT =  TreeNode("Drinks") 
leftChild = TreeNode("Hot") 
rightChild = TreeNode("Cold")
newBT.leftChild = leftChild 
newBT.rightChild = rightChild

def preOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    print(rootNode.data) #O(1)
    preOrderTraversal(rootNode.leftChild) #O(N/2)
    preOrderTraversal(rootNode.rightChild) #O(N/2)

def inOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    inOrderTraversal(rootNode.leftChild) #O(N/2)
    print(rootNode.data) #O(1)
    inOrderTraversal(rootNode.rightChild)   #O(N/2)

def postOrderTraversal(rootNode): 
    if not rootNode:  #O(1)
        return 
    postOrderTraversal(rootNode.leftChild) #O(N/2)
    postOrderTraversal(rootNode.rightChild) #O(N/2)
    print(rootNode.data) #O(1)

def levelOrderTraversal(rootNode): 
    if not rootNode:  #checking the rootnode #O(1)
        return
    else: 
        customQueue = queue.Queue()   #O(1)
        customQueue.enqueue(rootNode) #O(1)
        while not (customQueue.isEmpty()): #O(n)
            root = customQueue.dequeue() #O(1)
            print(root.value.data) 
            if (root.value.leftChild is not None): #O(1)
                customQueue.enqueue(root.value.leftChild) 
            if (root.value.leftChild is not None): #O(1)
                customQueue.enqueue(root.value.rightChild)

def searchBT(rootNode, nodeValue): 
    if not rootNode: 
        return "The BT does not exist" 
    else: 
        customQueue = queue.Queue() 
        customQueue.enqueue(rootNode) 
        while not (customQueue.isEmpty()): 
            root = customQueue.dequeue() 
            if root.value.data == nodeValue: 
                return "Success"
            if (root.value.leftChild is not None) : 
                customQueue.enqueue(root.value.leftChild) 
            if (root.value.leftChild is not None): 
                customQueue.enqueue(root.value.rightChild)
        return "Not found"

def insertNodeBT(rootNode, newNode): 
    if not rootNode: 
        rootNode = newNode
    else: 
        customQueue = queue.Queue() 
        customQueue.dequeue(rootNode)
        while not (customQueue.isEmpty()):
            root = customQueue.dequeue()
            if root.value.leftChild is not None: 
                customQueue.enqueue(root.value.leftChild)
            else: 
                root.value.leftChild = newNode 
                return "Successfully Inserted" 

            if root.value.rightChild is not None: 
                customQueue.enqueue(root.value.rightChild) 
            else: 
                root.vallue.leftChild = newNode 
                return "Successfully Inserted" 

def deleteDeepestNode (rootNode, dNode): 
    if not rootNode: 
        return 
    else: 
        customQueue = queue.Queue() 
        customQueue.enqueue(rootNode)
        while not (customQueue.isEmpty()):
            root = customQueue.dequeue()
            if root.value is dNode: 
                root.value = None 
                return 
            if root.value.rightChild: 
                if root.value.rightChild is dNode: 
                    root.value.rightChild = None 
                    return 
                else: 
                    customQueue.enqueue(root.value.rightChild) 
            if root.value.leftChild: 
                if root.value.leftChild is dNode: 
                    root.value.leftChild = None 
                    return 
                else: 
                    customQueue.enqueue(root.value.leftChild) 

def deleteNodesBT (rootNode, node): 
    if not rootNode: 
        return "The BT does not exist" 
    else: 
        customQueue = queue.Queue() 
        customQueue.enqueue(rootNode)
        while not (customQueue.isEmpty()):
            root = customQueue.dequeue()
            if root.value.data == node: 
                dNode = getDeepestNode(rootNode) 
                root.value.data = dNode.data 
                deleteDeepestNode(rootNode, dNode)
                return "The node has been successfully deleted" 

            if (root.value.leftChild is not None): #O(1)
                customQueue.enqueue(root.value.leftChild) 
            if (root.value.leftChild is not None): #O(1)
                customQueue.enqueue(root.value.rightChild)
        return "Failed to delete"

#newNode = getDeepestNode(newBT) 
#deleteDeepestNode(newBT, newNode)
#levelOrderTraversal(newBT)
deleteNodeBT(newBT, "Hot")
levelOrderTraversal(newBT)

Time complexity : O(N)

Space complexity : O(N)

Delete entire Binary Tree (Linked list)

The concept is very simple. We just have to set the following :

rootNode = None
rootNode.leftChild = None
rootNode.rightChild = None

When we do this, the children become eligible for garbage collection.

def deleteBT(rootNode): 
    rootNode = None 
    rootNode.leftChild = None 
    rootNode.rightChild = None 
    return "The BT has been successfully deleted"
deleteBT(newBT) 
levelOrderTraversal(newBT)

I've called levelOrderTraversal to see how this is working. If the code is correct, it will show None, means levelOrderTraversal is not possible.

Time complexity : O(N)

Space complexity : O(N)

Create Binary tree (Python list)

While creating a list, we will keep the cell of index 0 empty (for simplicity). Afterwards, index 1 will have N1, index 2 will have N2.

Math behind this: Left child = cell[2x] -> x =3(parent) , cell[2*3=6] (child)

Right child = cell[2x+1] -> x=3, cell[2*3 + 1 = 7]

def BinaryTree: 
    def __init__(self, size): 
        self.customList = size * [None] 
        self.lastUsedIndex = 0 
        self.maxSize = size 
newBT = BinaryTree(8)

Time complexity: O(1), Space complexity: O(N)

Insert a value Binary Tree (Python list)

While inserting, we usually face two situations:

The binary tree is full
We have to look for a first vacant place

We know that, we look for a vacant place using levelOrder traversal.

def BinaryTree: 
    def __init__(self, size): 
        self.customList = size * [None] 
        self.lastUsedIndex = 0 
        self.maxSize = size 
    def insertNode(self,value): 
        if self.lastUsedIndex + 1 == self.maxSize:  #O(1) 
            return "The binary tree is full" 
        self.customList[self.lastUsedIndex+1] = value  #O(1)
        self.lastUsedIndex += 1 #O(1)
        return "The value has been successfully inserted" 

newBT = BinaryTree(8)
print(newBT.insertNode("Drink"))
print(newBT.insertNode("Hot"))
print(newBT.insertNode("Cold")

Time complexity: O(1), Space complexity: O(1)

Search for a node in Binary Tree (Python list)

We look for a node using level order traversal. We will start from the root node.

def BinaryTree: 
    def __init__(self, size): 
        self.customList = size * [None] 
        self.lastUsedIndex = 0 
        self.maxSize = size 
    def insertNode(self,value): 
        if self.lastUsedIndex + 1 == self.maxSize:  #O(1) 
            return "The binary tree is full" 
        self.customList[self.lastUsedIndex+1] = value  #O(1)
        self.lastUsedIndex += 1 #O(1)
        return "The value has been successfully inserted" 
    def searchNode(self, nodeValue): 
        for i in range(len(self.customList)): 
            if self.customList[i] == nodeValue: 
                return "Success" 
        return "Not found"

newBT = BinaryTree(8)
print(newBT.insertNode("Drink"))
print(newBT.insertNode("Hot"))
print(newBT.insertNode("Cold")
print(newBT.searchNode("Tea"))
print(newBT.searchNode("Hot"))

Time complexity: O(n) [traversing takes o(n) time complexity], Space complexity: O(1)

PreOrder Traversal Binary Tree (Python list)

The logic behind preOrder traversal is: Root node -> Left subtree -> right subtree

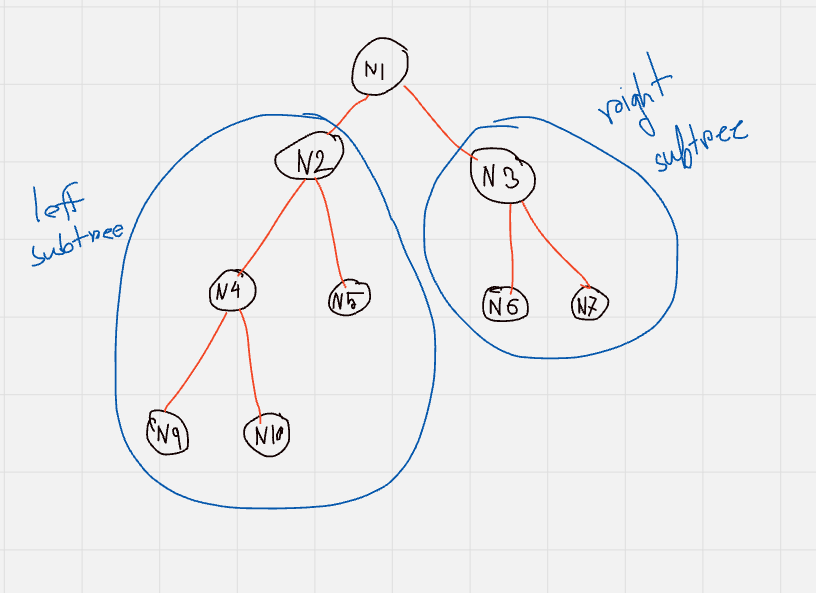
N1 -> N2 -> N4 -> N9 -> N10 -> N5 -> N3 -> N6 -> N7

def BinaryTree: 
    def __init__(self, size): 
        self.customList = size * [None] 
        self.lastUsedIndex = 0 
        self.maxSize = size 
    def insertNode(self,value): 
        if self.lastUsedIndex + 1 == self.maxSize:  #O(1) 
            return "The binary tree is full" 
        self.customList[self.lastUsedIndex+1] = value  #O(1)
        self.lastUsedIndex += 1 #O(1)
        return "The value has been successfully inserted" 
    def searchNode(self, nodeValue): 
        for i in range(len(self.customList)): 
            if self.customList[i] == nodeValue: 
                return "Success" 
        return "Not found"
    def preOrderTraversal(self, index): 
        if index > self.lastUsedIndex: 
            return 
        print(self.customList[index]) 
        self.preOrderTraversal(index * 2) 
        self.preOrderTraversal(index*2 + 1) 

newBT = BinaryTree(8)
print(newBT.insertNode("Drink"))
print(newBT.insertNode("Hot"))
print(newBT.insertNode("Cold")
print(newBT.searchNode("Tea"))
print(newBT.searchNode("Hot"))

newBT.preOrderTraversal(1)

Time complexity: O(N), Space complexity: O(1)

InOrder Traversal Binary Tree (Python list)

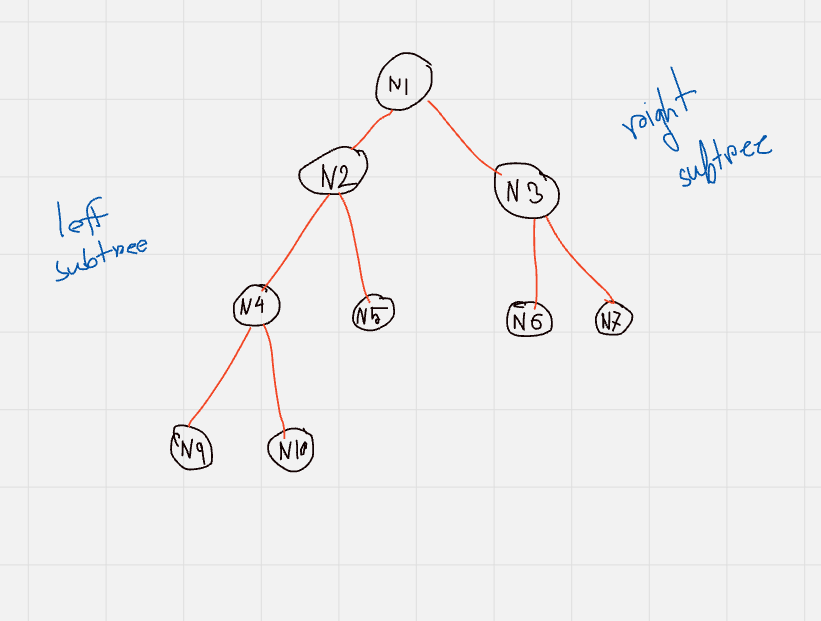
The logic behind preOrder traversal is: Left subtree -> Root node -> right subtree

def BinaryTree: 
    def __init__(self, size): 
        self.customList = size * [None] 
        self.lastUsedIndex = 0 
        self.maxSize = size 
    def insertNode(self,value): 
        if self.lastUsedIndex + 1 == self.maxSize:  #O(1) 
            return "The binary tree is full" 
        self.customList[self.lastUsedIndex+1] = value  #O(1)
        self.lastUsedIndex += 1 #O(1)
        return "The value has been successfully inserted" 
    def searchNode(self, nodeValue): 
        for i in range(len(self.customList)): 
            if self.customList[i] == nodeValue: 
                return "Success" 
        return "Not found"
    def preOrderTraversal(self, index): 
        if index > self.lastUsedIndex: 
            return 
        print(self.customList[index]) 
        self.preOrderTraversal(index * 2) 
        self.preOrderTraversal(index*2 + 1) 
    def inOrderTraversal(self, index): 
        if index > self.lastUsedIndex: 
            return
        self.inOrderTraversal(index*2) 
        print(self.customList[index])
        self.inOrderTraversal(index*2+1)


newBT = BinaryTree(8)
print(newBT.insertNode("Drink"))
print(newBT.insertNode("Hot"))
print(newBT.insertNode("Cold")
print(newBT.searchNode("Tea"))
print(newBT.searchNode("Hot"))

newBT.preOrderTraversal(1)
newBT.inOrderTraversal(1)

Time complexity: O(N), Space complexity: O(N)

PostOrder Traversal Binary Tree (Python list)

Left sub tree -> right subtree -> root node

def BinaryTree: 
    def __init__(self, size): 
        self.customList = size * [None] 
        self.lastUsedIndex = 0 
        self.maxSize = size 
    def insertNode(self,value): 
        if self.lastUsedIndex + 1 == self.maxSize:  #O(1) 
            return "The binary tree is full" 
        self.customList[self.lastUsedIndex+1] = value  #O(1)
        self.lastUsedIndex += 1 #O(1)
        return "The value has been successfully inserted" 
    def searchNode(self, nodeValue): 
        for i in range(len(self.customList)): 
            if self.customList[i] == nodeValue: 
                return "Success" 
        return "Not found"

    def preOrderTraversal(self, index): 
        if index > self.lastUsedIndex: 
            return 
        print(self.customList[index]) 
        self.preOrderTraversal(index * 2) 
        self.preOrderTraversal(index*2 + 1) 

    def inOrderTraversal(self, index): 
        if index > self.lastUsedIndex: 
            return
        self.inOrderTraversal(index*2) 
        print(self.customList[index])
        self.inOrderTraversal(index*2+1)

    def postOrderTraversal(self, index): 
        if index > self.lastUsedIndex: 
            return       
        self.postOrderTraversal(index*2)
        self.postOrderTraversal(index*2+1)
        print(self.customList[index])


newBT = BinaryTree(8)
print(newBT.insertNode("Drink"))
print(newBT.insertNode("Hot"))
print(newBT.insertNode("Cold")
print(newBT.searchNode("Tea"))
print(newBT.searchNode("Hot"))

newBT.preOrderTraversal(1) #index will be 1
newBT.inOrderTraversal(1) 
newBT.postOrderTraversal(1)

Time complexity: O(N), Space complexity: O(N)

LevelOrder Traversal Binary Tree (Python list)

def BinaryTree: 
    def __init__(self, size): 
        self.customList = size * [None] 
        self.lastUsedIndex = 0 
        self.maxSize = size 
    def insertNode(self,value): 
        if self.lastUsedIndex + 1 == self.maxSize:  #O(1) 
            return "The binary tree is full" 
        self.customList[self.lastUsedIndex+1] = value  #O(1)
        self.lastUsedIndex += 1 #O(1)
        return "The value has been successfully inserted" 
    def searchNode(self, nodeValue): 
        for i in range(len(self.customList)): 
            if self.customList[i] == nodeValue: 
                return "Success" 
        return "Not found"

    def preOrderTraversal(self, index): 
        if index > self.lastUsedIndex: 
            return 
        print(self.customList[index]) 
        self.preOrderTraversal(index * 2) 
        self.preOrderTraversal(index*2 + 1) 

    def inOrderTraversal(self, index): 
        if index > self.lastUsedIndex: 
            return
        self.inOrderTraversal(index*2) 
        print(self.customList[index])
        self.inOrderTraversal(index*2+1)

    def postOrderTraversal(self, index): 
        if index > self.lastUsedIndex: 
            return       
        self.postOrderTraversal(index*2)
        self.postOrderTraversal(index*2+1)
        print(self.customList[index])

    def levelOrderTraversal(self,index):
        for i in range(index, self.lastUsedIndex + 1): 
            print(self.customList[i])


newBT = BinaryTree(8)
print(newBT.insertNode("Drink"))
print(newBT.insertNode("Hot"))
print(newBT.insertNode("Cold")
print(newBT.searchNode("Tea"))
print(newBT.searchNode("Hot"))

newBT.preOrderTraversal(1) #index will be 1
newBT.inOrderTraversal(1) 
newBT.postOrderTraversal(1)
newBT.levelOrderTraversal(1)

Time complexity: O(N), Space complexity: O(N)

Delete a node from binary tree (Python list)

Here, the first thing we are going to do is find the deepest node in the tree. What's the deepest node in the tree? It is the last node when we use levelOrder traversal. In case of python list, is is located in the last index ( deepestNode = LastUsedIndex)

Let's say we want to delete the N3 node over here. We can't delete N3 directly as N6. N7 is dependent on N3. If their link gets broken, garbage collector will collect them. So, we will replace N3 with N9(the last node). This is our concept of deleting a node from a tree.

(previous code) 
    def deleteNode(self,value):
        if self.lastUsedIndex == 0: 
            return "there is not any node to delete" 
        for i in range(1, self.lastUsedIndex+1): 
            if self.customList[i] == value: 
                self.customList[i] = self.customList[self.lastUsedIndex]
                self.customList[self.lastUsedIndex] = None 
                self.lastUsedIndex -= 1
                return "The node has been successfully deleted"

newBT = BinaryTree(8)
print(newBT.insertNode("Drink"))
print(newBT.insertNode("Hot"))
print(newBT.insertNode("Cold")
print(newBT.searchNode("Tea"))
print(newBT.searchNode("Hot"))

newBT.deleteNode["Tea"]
newBT.levelOrderTraversal(1)

Time complexity: O(n), Space complexity: O(1)

Delete entire binary tree (Python list)

We have to update the following:

customList = None

def BinaryTree: 
    def __init__(self, size): 
        self.customList = size * [None] 
        self.lastUsedIndex = 0 
        self.maxSize = size 
    def insertNode(self,value): 
        if self.lastUsedIndex + 1 == self.maxSize:  #O(1) 
            return "The binary tree is full" 
        self.customList[self.lastUsedIndex+1] = value  #O(1)
        self.lastUsedIndex += 1 #O(1)
        return "The value has been successfully inserted" 
    def searchNode(self, nodeValue): 
        for i in range(len(self.customList)): 
            if self.customList[i] == nodeValue: 
                return "Success" 
        return "Not found"

    def preOrderTraversal(self, index): 
        if index > self.lastUsedIndex: 
            return 
        print(self.customList[index]) 
        self.preOrderTraversal(index * 2) 
        self.preOrderTraversal(index*2 + 1) 

    def inOrderTraversal(self, index): 
        if index > self.lastUsedIndex: 
            return
        self.inOrderTraversal(index*2) 
        print(self.customList[index])
        self.inOrderTraversal(index*2+1)

    def postOrderTraversal(self, index): 
        if index > self.lastUsedIndex: 
            return       
        self.postOrderTraversal(index*2)
        self.postOrderTraversal(index*2+1)
        print(self.customList[index])

    def levelOrderTraversal(self,index):
        for i in range(index, self.lastUsedIndex + 1): 
            print(self.customList[i])

    def deleteNode(self,value):
        if self.lastUsedIndex == 0: 
            return "there is not any node to delete" 
        for i in range(1, self.lastUsedIndex+1): 
            if self.customList[i] == value: 
                self.customList[i] = self.customList[self.lastUsedIndex]
                self.customList[self.lastUsedIndex] = None 
                self.lastUsedIndex -= 1
                return "The node has been successfully deleted"

    def deleteBT(self): 
        self.customList = None 
        return "The binary tree has been deleted successfully"

newBT = BinaryTree(8)
print(newBT.insertNode("Drink"))
print(newBT.insertNode("Hot"))
print(newBT.insertNode("Cold")
print(newBT.searchNode("Tea"))
print(newBT.searchNode("Hot"))

newBT.deleteNode["Tea"]
print(newBT.deleteBT())
newBT.levelOrderTraversal(1)Time complexity: O(n), Space complexity: O(1)

Time complexity: O(n), Space complexity: O(1)

End.

Tree/Binary Tree in Python DSA

Table of contents

What is a Tree?

Why Tree?

Tree Terminology

How to create basic tree in Python

__str__ function for Tree - explanation

Binary Tree

Types of Binary Tree

Binary Tree Representation

Create Binary Tree (Linked list)

PreOder Traversal Binary Tree (Linked list)

InOrder Traversal Binary Tree (Linked list)

PostOrder Traversal Binary Tree (Linked list)

LevelOrder Traversal Binary Tree (Linked list)

Searching for a node in Binary Tree (Linked list)

Inserting a node in Binary Tree (Linked list)

Delete a node from Binary Tree (Linked list)

Delete entire Binary Tree (Linked list)

Create Binary tree (Python list)

Insert a value Binary Tree (Python list)

Search for a node in Binary Tree (Python list)

PreOrder Traversal Binary Tree (Python list)

InOrder Traversal Binary Tree (Python list)

PostOrder Traversal Binary Tree (Python list)

LevelOrder Traversal Binary Tree (Python list)

Delete a node from binary tree (Python list)

Delete entire binary tree (Python list)

str function for Tree - explanation